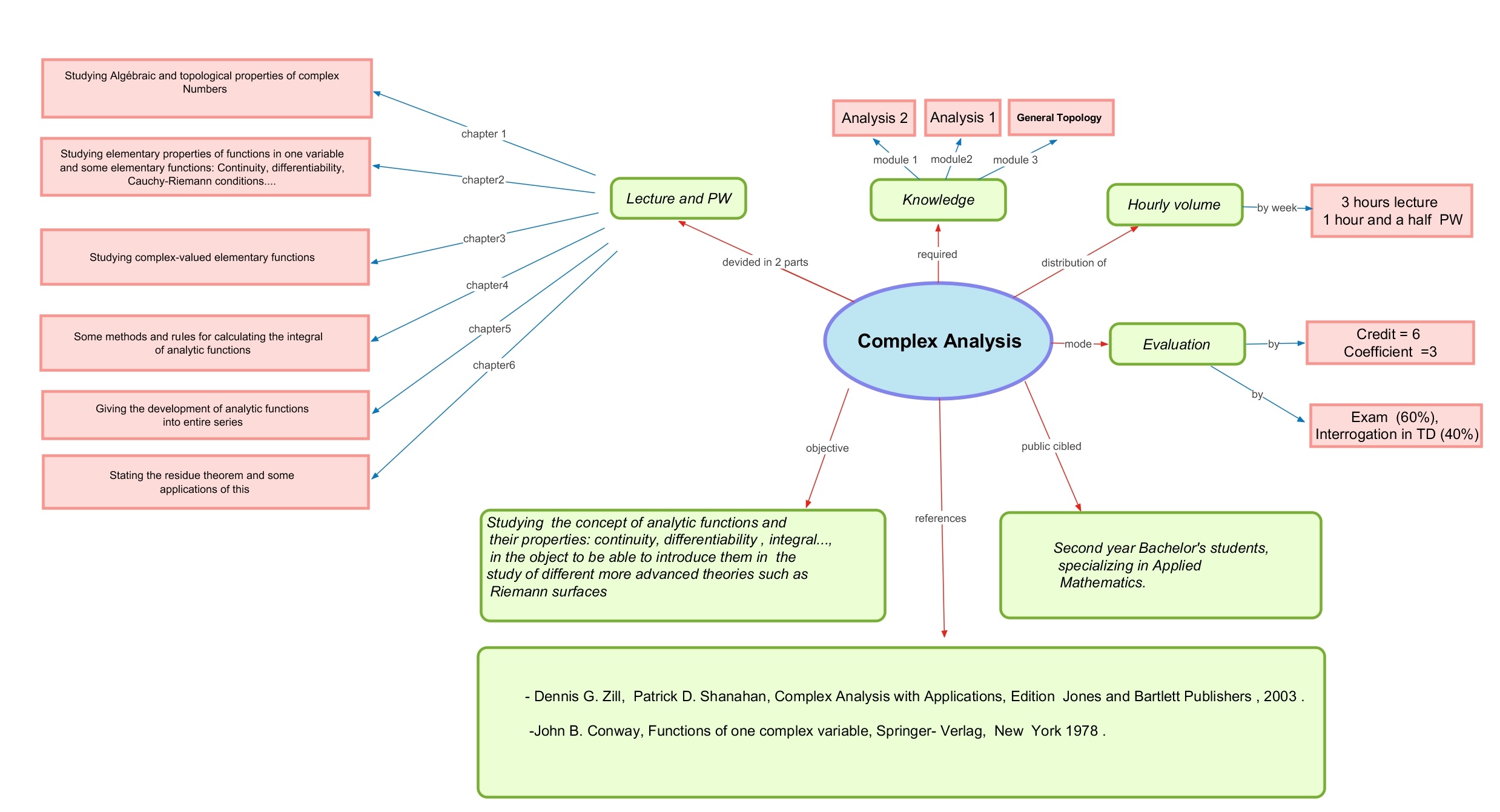
This course offers an in-depth introduction to the fundamental concepts of complex analysis. It is designed to help students master algebraic computations within the set of complex numbers and to understand the relationship between geometry and algebra in these operations. The course also aims to build a solid foundation in basic topological concepts related to complex numbers, preparing students for the study of functions of a complex variable and the associated analytical computations.
Learning Objectives:
- Understand the concept of complex numbers, their construction, and establish the connection between algebraic operations and their geometric interpretation.
- Perform algebraic operations on complex numbers, including addition, multiplication, conjugation, modulus, and argument.
- Understand the structure of the set of complex numbers as an extension of the field of real numbers.
- Solve polynomial equations in the set of complex numbers.
- Understand and apply the basic topological concepts of the complex plane to the study of complex functions such as continuity, differentiability, and analyticity.
- Acquire the properties of functions of one complex variable and apply calculus techniques related to these functions, including integration, residue calculus, and Laurent series.
- Prepare for more advanced theories: complex differential equations and Riemann surfaces.
- Dr: nabila belhamra